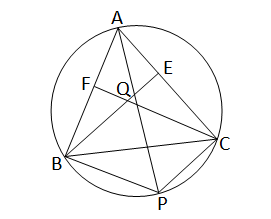
---

∆ABC একটি সূক্ষ্মকোণী ত্রিভূজ। ∆ABC এর পরিবৃত্তের ব্যাস AP;BE এবং CF যথাক্রমে AC এবং AB বাহুর উপর লম্ব এবং তারা পরস্পরকে Q বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,BPCQ একটি সামান্তরিক।

অঙ্কনঃ B,P এবং C,P যুক্ত করা হল।

প্রমানঃ যেহেতু,AP বৃত্তের ব্যাস
∴\(\angle\)ABP=90°
আবার \(\angle\)CFB=90°[∵CF,AB এর ওপর লম্ব]
∴FC∥BP অর্থাৎ,QC∥BP

আবার যেহেতু,AP বৃত্তের ব্যাস
∴\(\angle\)ACP=90°
আবার \(\angle\)BEC=90°[∵BE,AC এর ওপর লম্ব]
∴BE∥PC অর্থাৎ,BQ∥PC

এখন চতুর্ভূজ BPCQ এর
QC∥BP এবং BQ∥PC

∴BPCQ একটি সামান্তরিক । (প্রমানিত)