প্রমাণ করি যে, কোনো সমদ্বিবাহু ট্রাপিজিয়ামের সমান্তরাল বাহুদুটির যে-কোনো একটির সংলগ্ন কোণ দুটি সমান।
Loading content...
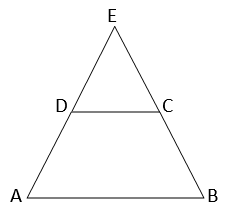
ধরি, \(ABCD\) একটি সমদ্বিবাহু ট্রাপিজিয়ম যার, \(AD=BC\)
প্রমান করতে হবে যে, \(∠ADC=∠BCD\)
অঙ্কনঃ \(AD\) এবং \(BC\) কে বর্ধিত করা হল,যারা পরস্পরকে \(E\) বিন্দুতে ছেদ করে।
প্রমানঃ \(∆EAB \) এর \(AB\) বাহুর সমান্তরাল সরলরেখা \(DC, EA \) এবং \(EB\) কে যথাক্রমে \( D\) এবং \( E\) বিন্দুতে অন্তর্বিভক্ত করেছে।
\(∴ \cfrac{ED}{AD}=\cfrac{EC}{BC} \)
বা, \(\cfrac{ED}{AD}=\cfrac{EC}{AD} [∵ AD=BC] \)
\(∴ ED=EC\)
\(∴ ∆EDC\) এর \(ED=EC\)
\(∴ ∠EDC=∠ECD\)
বা, \((180°-∠ADC)=(180°-∠BCD)\)
অর্থাৎ, \(∠ADC=∠BCD\) (প্রমানিত)