দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। P ও Q বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও C এবং অপর বৃত্তকে যথাক্রমে B ও D বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, AC || BD।
Loading content...
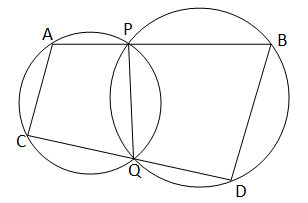
দুটি বৃত্ত পরস্পরকে P এবং Q বিন্দুতে ছেদ করেছে। P এবং Q বিন্দু দিয়ে অঙ্কিত দুটি সরলরেখা বৃত্তদুটিকে যথাক্রমে A,C ও B,D বিন্দুতে ছেদ করেছে ।
প্রমান করতে হবে যে,AC∥BD
প্রমানঃ ACQP একটি বৃত্তস্থ চতুর্ভূজ।
∴\(\angle\)ACQ+\(\angle\)APQ=2 সমকোণ
আবার যেহেতু AB সরল্রেখার ওপর P বিন্দুতে PQ দন্ডায়মান,
তাই \(\angle\)APQ+\(\angle\)BPQ=2 সমকোণ
∴ \(\angle\)ACQ+\(\angle\)APQ=\(\angle\)APQ+\(\angle\)BPQ
অর্থাৎ,\(\angle\)ACQ=\(\angle\)BPQ
আবার,BPQD একটি বৃতস্থ চতুর্ভূজ
∴\(\angle\)BDQ+\(\angle\)BPQ=2 সমকোণ
বা,\(\angle\)BDQ+\(\angle\)ACQ=2 সমকোণ [\(\angle\)ACQ=\(\angle\)BPQ বসিয়ে]
∵ AC এবং BD দুটি সরলরেখাকে CD ভেদক ছেদ করায় একই পার্শ্বস্থ দুটি কোণ \(\angle\)BDQ এবং \(\angle\)ACQ উৎপন্ন হয় এবং যাদের সমষ্টি 2 সমকোণ ।
তাই AC∥BD (প্রমানিত)