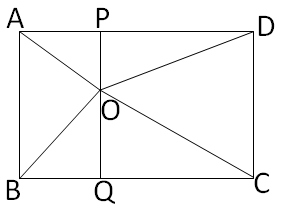
---

O বিন্দু দিয়ে AB এর সমান্তরাল সরলরেখা PQ অঙ্কন করা হল ।
\(\triangle\)BOQ থেকে পাই, OB\(^2\)=BQ\(^2\)+OQ\(^2\)------(i)
\(\triangle\)POD থেকে পাই, OD\(^2\)=PD\(^2\)+OP\(^2\)------(ii)
\(\because\)ABCD একটি আয়তক্ষেত্র এবং PQ সমান্তরাল AB
সুতরাং, AP=BQ এবং PD=QC

(i) এবং (ii) নং সমীকরন যোগ করে পাই,
OB\(^2\)+OD\(^2\)=BQ\(^2\)+OQ\(^2\)+PD\(^2\)+OP\(^2\)
বা, OB\(^2\)+OD\(^2\)=AP\(^2\)+OQ\(^2\)+QC\(^2\)+OP\(^2\)
বা, OB\(^2\)+OD\(^2\)=AP\(^2\)+OP\(^2\)+OQ\(^2\)+QC\(^2\)

=OA\(^2\)+OC\(^2\)

\(\therefore\) 6\(^2\)+8\(^2\)=5\(^2\)+OC\(^2\)
বা, OC\(^2\)=36+64-25=75
বা, OC=√75=5√3

\(\therefore\) OC এর দৈর্ঘ্য 5√3 সেমি ।