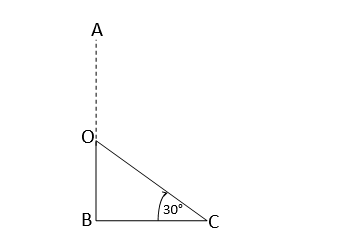
---

ধরি,AB একটি 126 ডেসিমি উঁচু একটি উল্লম্ব খুঁটি, যার মাটি থেকে কিছু উপরে O বিন্দুতে দুমড়ে গিয়ে তার অগ্রভাগ A বিন্দু C বিন্দুতে স্পর্শ করেছে। এবং ভূমির সঙ্গে উৎপন্ন কোণ ∠OCB=30°

সমকোণী ত্রিভূজ OBC থেকে পাই
tan30°=লম্ব/ভূমি \(=\frac{OB}{BC}\)
বা, \(\frac{1}{√3}=\frac{OB}{BC} \)
বা,OB\(=\frac{BC}{√3}----(i) \)

আবার,cos30°=ভূমি /অতিভূজ \(=\frac{BC}{OC}\)
বা, \(\frac{√3}{2}=\frac{BC}{OC}\)
বা, OC\(=\frac{2BC}{√3}---(ii)\)

∵উল্লম্ব খুঁটিটির উচ্চতা,AB=126
বা,AO+OB=126
বা,OC+OB=126 [∵AO=OC]
বা, \(\frac{2BC}{√3}+\frac{BC}{√3}=126\) [\((ii)\) এবং \((i) \) নং থেকে]
বা, \(BC(\frac{2}{√3}+\frac{1}{√3})=126\)
বা, \(BC×\frac{3}{√3}=126\)
বা, \(BC=\frac{126√3}{3}=42√3\)

(i) নং সমীকরনে BC এর মান বসিয়ে পাই
OB\(=\frac{42√3}{√3}=42\)

∴খুঁটিটি মাটি থেকে OB=42 ডেসিমি উচ্চতায় দুমড়ে গিয়েছিল এবং তা মাটি থেকে BC=42√3 ডেসিমি দূরে মাটি স্পর্শ করেছিল ।