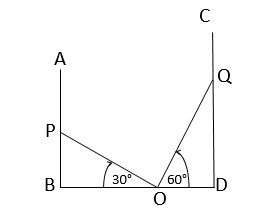
---

মনে করি BD রাস্তার দু-পাশে AB এবং CD দুটি বাড়ি আছে । প্রথম বাড়ির গোড়া B বিন্দু থেকে 6 মিটার দূরে O বিন্দুতে মইটির গোড়া রেখে মইটিকে প্রথম বাড়ির দেওয়ালে ঠেকালে তা P বিন্দুতে এবং দ্বিতীয় বাড়িতে ঠেকালে তা Q বিন্দুতে স্পর্শ করে ।
∴PO=6 মিটার এবং ∠POB=30° এবং ∠QOD=60°

∴ত্রিভূজ PBO থেকে ∠POB এর পরিপ্রেক্ষিতে পাই
cos30°=ভূমি/অতিভূজ \(=\frac{BO}{PO}=\frac{6}{PO}\)
বা,cos30° \(=\frac{6}{PO}\)
বা, \(\frac{√3}{2}=\frac{6}{PO}\)
বা, PO \(=\frac{6×2}{√3}=\frac{12×√3}{√3×√3}=\frac{12√3}{3}=4√3\)

আবার OQ=মইয়ের দৈর্ঘ্য=OP=4√3 মিটার
∴ ত্রিভূজ QOD থেকে ∠QOD এর পরিপ্রেক্ষিতে পাই
cos60°=ভূমি/অতিভূজ \(=\frac{OD}{OQ}=\frac{OD}{4√3}\)
বা,cos60° \(=\frac{OD}{4√3}\)
বা, \(\cfrac{1}{2}=\frac{OD}{4√3}\)
বা,OD \(=\frac{4√3}{2}=2√3\)

∆OQD থেকে পাই,
\(\frac{QD}{OD}=tan⁡ 60°\)
বা, \(\frac{QD}{2√3}=√3\)
বা,QD=6

(i)মইটির দৈর্ঘ্য=OP=4√3 মিটার
(ii)দ্বিতীয় বাড়ির গোড়া থেকে মইটির গোড়ার দূরত্ব 2√3 মিটার ।
(iii) রাস্তাটি চওড়া=BD=BO+OD =6+2√3 মিটার=2(3+√3) মিটার।
(iv) দ্বিতীয় বাড়িটির QD=6 মিটার উঁচুতে মইটি স্পর্শ করবে।