প্রমাণ করি, যে-কোনো রম্বসের বাহুগুলির উপর অঙ্কিত বর্গের সমষ্টি কর্ণ দুটির উপর অঙ্কিত বর্গ দুটির সমষ্টির সমান হবে।
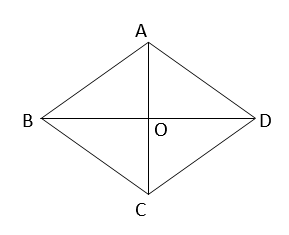
ধরি,ABCD রম্বসের দুটি কর্ণ AC এবং BD পরস্পরকে O বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,AB\(^2\)+BC\(^2\)+CD\(^2\)+DA\(^2\)=AC\(^2\)+BD\(^2\)
∵রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে,তাই ∆AOB,∆BOC,∆COD,∆DOA প্রত্যেকে সমকোণী ত্রিভূজ এবং রম্বসের বাহুগুলি ঐ ত্রিভূজের অতিভূজ।
∴ AB\(^2\)+BC\(^2\)+CD\(^2\)+DA\(^2\)
=(AO\(^2\)+OB\(^2\) )+(BO\(^2\)+OC\(^2\) )
+(OC\(^2\)+OD\(^2\) )+(OD\(^2\)+OA\(^2\) )
=2OA\(^2\)+2BO\(^2\)+2OC\(^2\)+2OD\(^2\)
=4OA\(^2\)+4OB\(^2\) [∵OA=OC এবং BO=OD]
=(2OA)\(^2\)+(2OB)\(^2\)
=AC\(^2\)+BD\(^2\) (প্রমানিত)