পিথাগোরাসের উপপাদ্যটি বিবৃত করো ও প্রমাণ করো
Loading content...
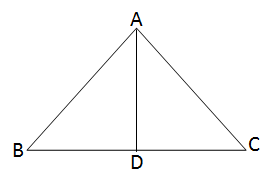
পিথাগোরাসের উপপাদ্য: যে-কোনো সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমষ্টির সমান।
প্রদত্ত : \(ABC\) একটি সমকোণী ত্রিভুজ যার \(∠A\) সমকোণ
প্রমাণ করতে হবে :\( BC^2 = AB^2 + AC^2\)
অঙ্কন : সমকৌণিক বিন্দু \(A\) থেকে অতিভুজ \(BC\)-এর উপর \(AD\) লম্ব অঙ্কন করলাম যা \(BC\) বাহুকে \(D\) বিন্দুতে ছেদ করে।
প্রমাণ : সমকোণী ত্রিভুজ \(ABC\)-এর অতিভুজ \(BC\)-এর উপর \(AD\) লম্ব।
\(∴ ∆ABD\) ও \(∆CBA\) সদৃশ।
সুতরাং, \(\cfrac{AB}{BC} = \cfrac{BD}{AB}\)
\(∴ AB^2 = BC.BD ......(I)\)
আবার, \(∆CAD\) ও \(∆CBA\) সদৃশ।
সুতরাং, \(\cfrac{AC}{BC} = \cfrac{DC}{AC}……….(II)\)
সুতরাং \((I)\) ও \((II)\) যোগ করে পাই,
\(AB^2 + AC^2 = BC.BD + BC.DC\)
\(= BC (BD + DC)\)
\(= BC.BC = BC^2\)
\(∴BC^2 = AB^2 + AC^2 \) [প্রমাণিত]
