প্রমাণ করি যে, কোনো ত্রিভুজের একটি বাহুর মধ্যবিন্দু দিয়ে অঙ্কিত দ্বিতীয় বাহুর সমান্তরাল সরলরেখা তৃতীয় বাহুকে সমদ্বিখণ্ডিত করে। [থ্যালেসের উপপাদ্যের সাহায্যে প্রমাণ করি]
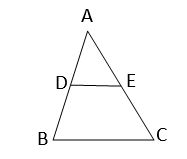
ধরি, \(∆ABC\) এর \(AB\) বাহুর মধ্যবিন্দু \(D\) দিয়ে অঙ্কিত দ্বিতীয় বাহু \(BC\) এর সমান্তরাল সরলরেখা তৃতীয় বাহু \(AC\) কে \(E\) বিন্দুতে ছেদ করে।
প্রমান করতে হবে যে, \(E,AC\) এর মধ্যবিন্দু।
প্রমানঃ∵ \(DE∥BC\)
∴থ্যালেসের উপপাদ্যের সাহায্যে পাই
\(\cfrac{AD}{DB}=\cfrac{AE}{EC}\)
বা, \(\cfrac{DB}{DB}=\cfrac{AE}{EC}\)
বা, \(1=\cfrac{AE}{EC} \)
অর্থাৎ, \(AE=EC\)
\(∴ E,AC\) বাহুর মধ্যবিন্দু [প্রমানিত]