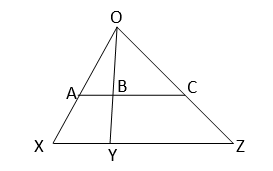
---

ধরি, \(OX,OY\) এবং \(OZ\) তিনটি সমবিন্দু সরলরেখা,যার \(O\) সমবিন্দু । \(AC\) এবং \(XZ\) দুটি সমান্তরাল সরলরেখা সরলরেখা তিনটিকে যথাক্রমে \(A,B,C\) এবং \(X,Y,Z\) বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে, \(AB:BC=XY:YZ\)

প্রমানঃ \(∆OXY\) এর \(XY∥AB\)
\(∴∠OAB=∠OXY\) [অনুরূপ কোণ]
এবং \(∠OBA=∠OYX\) [অনুরূপ কোণ]

এখন \(∆OAB\) এবং \( ∆OXY\) এর মধ্যে
\(∠OAB=∠OXY\) এবং \(∠OBA=∠OYX\)
\(∴∆OAB\) ও \( ∆OXY\) সদৃশকোণী
\(∴\cfrac{OA}{OX}=\cfrac{OB}{OY}=\cfrac{AB}{XY}----(i)\)

অনুরূপভাবে প্রমান করা যায় যে, \(∆OBC\) এবং \(∆OYZ\) সদৃশকোণী।

\(∴ \cfrac{OB}{OY}=\cfrac{OC}{OZ}=\cfrac{BC}{YZ}----(ii)\)

\((i)\) এবং \( (ii)\) নং থেকে পাই,
\(\cfrac{OA}{OX}=\cfrac{OB}{OY}=\cfrac{OC}{OZ}=\cfrac{AB}{XY}=\cfrac{BC}{YZ} \)
অর্থাৎ, \(\cfrac{AB}{XY}=\cfrac{BC}{YZ} \)
বা, \(\cfrac{AB}{BC}=\cfrac{XY}{YZ} \)
অর্থাৎ, \(AB:BC=XY:YZ\) (প্রমানিত)