একটি O কেন্দ্রীয় বৃত্ত অঙ্কন করি যার দুটি ব্যাসার্ধ OA ও OB পরস্পর লম্বভাবে অবস্থিত। A ও B বিন্দুতে অঙ্কিত স্পর্শকদ্বয় পরস্পরকে T বিন্দুতে ছেদ করলে, প্রমাণ করি যে, AB = OT এবং তারা পরস্পরকে লম্বভাবে সমদ্বিখণ্ডিত করে।
Loading content...
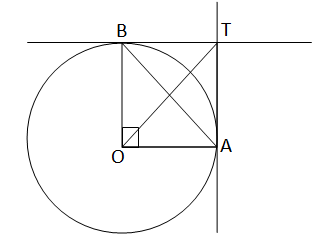
O কেন্দ্রীয় বৃত্ত,যার দুটি ব্যাসার্ধ OA এবং OB পরস্পর লম্বভাবে অবস্থিত। A এবং B বিন্দুতে স্পর্শকদ্বয় পরস্পর কে T বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে, AB=OT এবং তারা পরস্পরকে লম্বভাবে সমদ্বিখন্ডিত করে।
প্রমানঃ AOBT চতুর্ভূজের,
OA⊥OB (প্রদত্ত)
এবং OA⊥AT[∵A বিন্দুতে AT বৃত্তের স্পর্শক]
এবং OB⊥BT[∵ B বিন্দুতে BT বৃত্তের স্পর্শক]
এবং OA=OB [ বৃত্তের ব্যাসার্ধ]
∴AOBT একটি বর্গক্ষেত্র
∴AB=OT [∵বর্গক্ষেত্রের কর্ণদ্বয় সমান]
এবং যেহেতু বর্গক্ষেত্রের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখণ্ডিত করে,
∴AB এবং OT পরস্পরকে লম্বভাবে সমদ্বিখন্ডিত করে। (প্রমানিত)