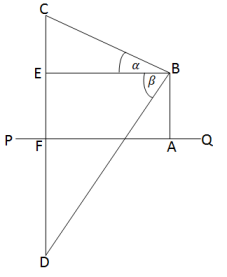
---

ধরি, \(PQ\) হ্রদের \(A\) বিন্দু থেকে \(h\) মিটার ওপর একটি বিন্দু \(B\) থেকে কোনো মেঘ \(C\) বিন্দুর উন্নতি কোণ \(\angle EBC =\alpha\) এবং হ্রদের ওপর ওর প্রতিবিম্ব \(D\) বিন্দুর অবনতি কোণ \(\angle EBD =β\) এবং যে বিন্দু থেকে মেঘ দেখা যাচ্ছে সেখান থেকে মেঘের দূরত্ব \(BC\)
\(\triangle BEC\) থেকে পাই,
\(\cfrac{CE}{BE}=tan\alpha\)
বা, \(CE=BE. tan\alpha\)------(i)

\(\triangle BDE\) থেকে পাই,
\(\cfrac{DE}{BE}=tan\beta\)
বা, \(DE=BE.tan\beta\)
বা, \(DF+EF=BE.tan\beta\)
যেহেতু, হ্রদের জলতল থেকে মেঘের উচ্চতা=জলতল থেকে প্রতিবিম্বের দূরত্ব
\(\therefore\) DF=CF
এবং, EF=AB=h মিটার
\(\therefore CF+h=BE tab\beta\)
বা, \(CE+EF+h=BE. tan\beta\)
বা, \(CE+h+h=BE. tan\beta\)
বা, \(CE+2h=BE. tan\beta\)
(i) নম্বরের \(CE\) এর মান বসিয়ে পাই,
\(BE.tan \alpha +2h=BE. tan\beta\)
বা, \(2h=BE. tan\beta-BE.tan \alpha\)
বা, \(BE(tan\beta-tan \alpha)=2h\)
বা, \(BE=\cfrac{2h}{tan\beta-tan \alpha}\)------(ii)

এখন, \(\triangle BEC\) থেকে পাই,
\(\cfrac{BC}{BE}=sec \alpha\)
বা, \(BC=BE.sec\alpha\)
\(\therefore BC=\cfrac{2h sec\alpha}{tan\beta-tan \alpha}\) [(ii) নম্বরের \(BE\) এর মান বসিয়ে] (প্রমাণিত)