16 সেমি. দৈর্ঘ্যের ব্যাসবিশিষ্ট একটি বৃত্তের কেন্দ্র থেকে 17 সেমি. দূরত্বে অবস্থিত বহিঃস্থ একটি বিন্দু থেকে অঙ্কিত বৃত্তের স্পর্শকের দৈর্ঘ্য হিসাব করে লিখি।
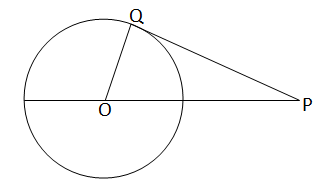
ধরি,O কেন্দ্রীয় বৃত্তের কেন্দ্র O থেকে OP=17 সেমি দূরে অবস্থিত বিন্দু P বিন্দু থেকে বৃত্তের ওপর স্পর্শক PQ;
OQ=বৃত্তের ব্যাসার্ধ=\(\frac{16}{2}\) সেমি=8 সেমি।
∴সমকোণী ∆OPQ এর,
OQ\(^2\)+QP\(^2\)=OP\(^2\) [পিথাগোরাসের উপপাদ্য থেকে]
বা,8\(^2\)+QP\(^2\)=17\(^2\)
বা,QP\(^2\)=289-64=225
বা,OP=\(\sqrt{225}\)=15
∴স্পর্শকের দৈর্ঘ্য=15 সেমি (Answer)