O কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ করি যে, BD\(^2\)=AD.DC
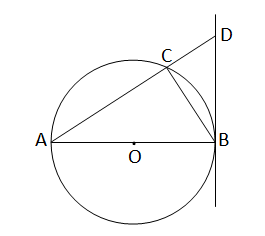
ধরি,O কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করেছে। প্রমান করতে হবে যে, BD\(^2\)=AD.DC
অঙ্কনঃ B,C যুক্ত করা হল।
প্রমানঃ যেহেতু ∠ACB=1 সমকোণ[অর্ধবৃত্তস্থ কোণ]
∴∆ACB সমকোণী ত্রিভূজ।
আবার,AB ব্যাসের B বিন্দুতে BD স্পর্শক,সুতরাং
∠ABD=1 সমকোণ।
∴∆ABD একটি সমকোণী ত্রিভূজ।
আবার,∆ABD এর সমকৌনিক বিন্দু B থেকে অতিভূজ AD এর উপর BC লম্ব।
∴∆ABD ও ∆BCD সদৃশ
∴ \(\frac{BD}{AD}=\frac{DC}{BD}\)
বা, BD\(^2\)=AD.DC [প্রমানিত]