O কেন্দ্রবিশিষ্ট একটি বৃত্তের AB একটি ব্যাস। P বৃত্তের উপর যে-কোনো একটি বিন্দু। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে P বিন্দুতে অঙ্কিত স্পর্শকটি যথাক্রমে Q ও R বিন্দুতে ছেদ করেছে। যদি বৃত্তের ব্যাসার্ধ r হয়, প্রমাণ করি যে, PQ.PR = r\(^2\)
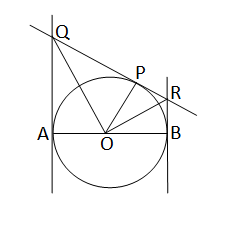
ধরি,O কেন্দ্রীয় বৃত্তের AB ব্যাস। P বৃত্তের ওপর যেকোনো একটি বিন্দু। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে P বিন্দুতে অঙ্কিত স্পর্শকটি যথাক্রমে Q এবং R বিন্দুতে ছেদ করেছে। যদি বৃত্তের ব্যাসার্ধ r হয় তবে প্রমান করতে হবে যে,PQ.PR=r\(^2\)
অঙ্কনঃ O,Q;O,P;O,R যুক্ত করা হল।
প্রমানঃ ∆AOQ এবং ∆OPQ এর
∠OAQ=∠OPQ [উভয়েই সমকোণ]
AO=OP [বৃত্তের ব্যাসার্ধ]
OQ সাধারন
∴∆AOQ≅∆OPQ
∴∠AOQ=∠POQ---(i)
অনুরূপভাবে ∆OBR এবং ∆POR থেকে প্রমান করা
যায় যে,∠BOR=∠POR---(ii)
(i)এবং (ii)নং সমীকরন যোগ করে পাই,
∠AOQ+∠BOQ=∠POQ+∠POR
আবার, ∠AOQ+∠BOQ+∠POQ+∠POR=180°
বা,2(∠POQ+∠POR)=180°
বা,∠POQ+∠POR=90°
বা,∠ROQ=90°
এখন ∆ROQ এর সমকৌনিক বিন্দু O থেকে অতিভূজ QR এর ওপর OP লম্ব।
∴OP\(^2\)=PQ.PR
ত্রিভূজের ব্যাসার্ধ r হলে OP=r
অর্থাৎ,PQ.PR=r\(^2\) (প্রমানিত)