প্রমাণ করাে যে, ব্যাস নয় এরূপ কেনাে জ্যা-কে বৃত্তের কেন্দ্রগামী কোনাে সরলরেখাংশ সমদ্বিখণ্ডিত করলে, ঐ সরলরেখাংশ জ্যা-এর উপর লম্ব হবে।

প্রমাণ করাে যে, ব্যাস নয় এরূপ কেনাে জ্যা-কে বৃত্তের কেন্দ্রগামী কোনাে সরলরেখাংশ সমদ্বিখণ্ডিত করলে, ঐ সরলরেখাংশ জ্যা-এর উপর লম্ব হবে। Madhyamik 2016 , 2012

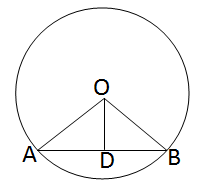
ধরি, O কেন্দ্রীয় বৃত্তের ব্যাস নয় এরূপ একটি জ্যা AB এবং D, AB এর মধ্যবিন্দু অর্থাৎ AD=DB
প্রমান করতে হবে যে OD\(\bot\)AB অর্থাৎ OD, AB জ্যা-এর ওপর লম্ব ।

অঙ্কন : O,A এবং O,B যুক্ত করা হল ।

প্রমান: \(\triangle\)OAD ও \(\triangle\)OBD এর মধ্যে
OA=OB [ একই বৃত্তের ব্যাসার্ধ]
AD=DB[প্রদত্ত] [D,AB এর মধ্যবিন্দু]
এবং OD সাধারন বাহু ।
\(\therefore \triangle\)OAD\(\cong \triangle\)ODB [সর্বসমতার S-S-S শর্তানুসারে]

\(\therefore \angle\)ODA=\(\angle\)ODB [অনুরূপ কোণ]
যেহেতু, OD, AB জ্যা এর ওপর দন্ডায়মান হয়ে সমান কোণ উৎপন্ন করেছে,
সুতরাং, \(\angle\)ODA=\(\angle\)ODB=1 সমকোণ
\(\therefore\) OD\(\bot\)AB [প্রমাণিত]