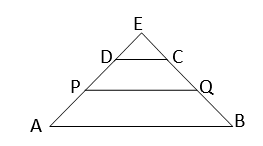
---

ধরি, \(ABCD\) ট্রাপিজিয়ামের \(AD\) এবং \(BC\) বাহুর মধ্যমা যথাক্রমে \(P\) এবং \(Q\) ;
প্রমান করতে হবে যে, \(PQ∥AB\) এবং \(PQ∥DC \)

অঙ্কনঃ \(AD \) এবং \(BC\) বাহুকে বর্ধিত করা হল,যারা পরস্পরকে \(E\) বিন্দুতে ছেদ করল।

প্রমানঃ \(∆EAB\) থেকে পাই,
\(DC∥AB\)
\(∴ \cfrac{EA}{AD} = \cfrac{EB}{BC}\)
বা, \(\cfrac{EA}{2AP}=\cfrac{EB}{2BQ} \)
বা, \(\cfrac{EA}{AP}=\cfrac{EB}{BQ}\)
\(∴ AB∥PQ \) (প্রমানিত)

আবার, \(∆EAB\) থেকে পাই
\(DC∥AB\)
\(∴ \cfrac{ED}{DA}=\cfrac{EC}{CB}\)
বা, \(\cfrac{ED}{2DP}=\cfrac{EC}{2CQ}\) [ \(∵ P \) ও \(Q\) যথাক্রমে \(AD\) ও \(BC\) এর মধ্যবিন্দু)]
বা, \(\cfrac{ED}{DP}=\cfrac{EC}{CQ} \)
\(∴ ∆EPQ \) থেকে পাই, \(\cfrac{ED}{DP}=\cfrac{EC}{CQ}\)
\(∴ PQ∥DC\) (প্রমানিত)