একটি বৃত্তস্থ চতুর্ভুজ ABCD-এর বর্ধিত AB ও DC বাহুদ্বয় পরস্পরকে P বিন্দুতে ছেদ করলে প্রমাণ করো যে, PA.PB=PC.PD
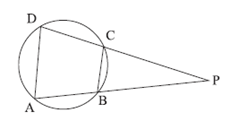
প্রদত্ত : \(ABCD\) বৃত্তস্থ চতুর্ভূজের বর্ধিত \(AB\) ও \(DC\) বাহুদ্বয় পরস্পরকে \(P\) বিন্দুতে ছেদ করে।
প্রমান করতে হবে : \(PA.PB=PC.PD\)
প্রমান : \(ABCD\) বৃত্তস্থ চতুর্ভূজ
\(∴ ∠DAB+∠DCB=180° \)
আবার, \(∠DCB+∠BCP=180° \)
\(∴ ∠DAB+∠DCB=∠DCB+∠BCP\)
\(∴ ∠DAB=∠BCP--------(I)\)
\(∆APD\) ও \(∆CPB\) এর,
\(∠APD=∠CPB\) [একই কোণ]
এবং \(∠PAD=∠BCP\) [\((I)\) থেকে পেলাম]
\(∴ ∆APD\) ও \(∆CPB\) সদৃশকোণী
সুতরাং, \(∆APD\) ও \(∆CPB\) সদৃশ
\(∴ \cfrac{PA}{PC}=\cfrac{PD}{PB} \)
সুতরাং \(PA.PB=PC.PD\) (প্রমানিত)