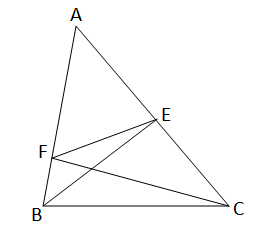
---

∆ABC এর AC এবং AB বাহুর ওপর যথাক্রমে BE ও CF লম্ব ।
প্রমান করতে হবে যে,B,C,E,F বিন্দু চারটি সমবৃত্তস্থ।

অঙ্কনঃ E,F যোগ করা হল।

প্রমানঃ \(\angle\)CEB=1 সমকোণ
এবং \(\angle\)BFC=1 সমকোণ
∴একই রেখাংশ BC এর ওপর অবস্থিত দুটি কোণ
\(\angle\)CEB=\(\angle\)BFC=1 সমকোণ
∴B,C,E,F বিন্দু চারটি সমবৃত্তস্থ (প্রমানিত)

---

∆AEF এবং ∆ABC থেকে পাই,
∵B,C,E,F বিন্দু চারটি সমবৃত্তস্থ

∴বৃত্তস্থ চতুর্ভূজ BCEF এর
বহিঃস্থ\(\angle\)AEF=বিপরীত \(\angle\)FBC
এবং বহিঃস্থ \(\angle\)AFE=বিপরীত \(\angle\)ECB

∆AEF এবং ∆ABC থেকে পাই,
\(\angle\)AEF=\(\angle\)ABC
[\(\angle\)FBC=\(\angle\)ABC(একই কোণ)
\(\angle\)AFE=\(\angle\)ACB [\(\angle\)ECB=\(\angle\)ACB(একই কোণ)

∴∆AEF ও ∆ABC এর দুটি করে কোণ সমান (প্রমানিত)