O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে অঙ্কিত দুটি স্পর্শক AP ও AQ বৃত্তকে P ও Q বিন্দুতে স্পর্শ করে। PR একটি ব্যাস হলে, প্রমাণ করি যে, OA || RQ
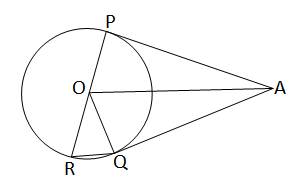
O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে অঙ্কিত দুটি স্পর্শক AP এবং AQ বৃত্তকে P ও Q বিন্দুতে স্পর্শ করেছে। PR ব্যাস হলে প্রমান করতে হবে যে, OA∥RQ
অঙ্কনঃ O,A এবং O,Q যুক্ত করা হল ।
প্রমানঃ ∆APO এবং ∆AQO এর মধ্যে
AP=AQ[ যেহেতু বহিঃস্থ বিন্দু থেকে দুটি স্পর্শক]
\(\angle\)APO=\(\angle\)AQO [উভয়েই সমকোণ]
এবং AO সাধারন।
∴∆APO≅∆AQO
সুতরাং,\(\angle\)POA=\(\angle\)QOA (অনুরূপ কোণ)
∆ORQ এর OQ=OR [বৃত্তের ব্যাসার্ধ]
∴\(\angle\)ORQ=\(\angle\)OQR
এবং \(\angle\)QOR=180°-( \(\angle\)ORQ+\(\angle\)OQR)=180°-2\(\angle\)OQR---(i)
আবার,\(\angle\)POA+\(\angle\)QOA+\(\angle\)QOR=180°
বা,2\(\angle\)QOA+\(\angle\)QOR=180°
অর্থাৎ,\(\angle\)QOR=180°-2\(\angle\)QOA---(ii)
(i)এবং (ii)নং সমীকরন থেকে পাই,
180°-2\(\angle\)OQR=180°-2\(\angle\)QOA
অর্থাৎ,\(\angle\)OQR=\(\angle\)QOA
আবার,OA এবং RQ সরলরেখা OR ভেদ করার জন্য দুটি সমান কোণ উৎপন্ন করেছে ।
∴OA∥RQ (প্রমানিত)