সূর্যের উন্নতি কোণ 45° থেকে 60°-তে পরিবর্তিত হলে, একটি স্তম্ভের ছায়ার দৈর্ঘ্য 30 মিটার কমে যায়। স্তম্ভটির উচ্চতা নির্ণয় করো।
Loading content...
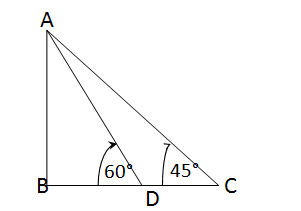
মনে করি,AB একটি স্তম্ভ, সূর্যের উন্নতি কোণ যখন 45° ছিল তখন ∠ACB =45° এবং ছায়ার দৈর্ঘ্য ছিল BC,যখন উন্নতিকোন 60° হয়,তখন ∠ADB=60° এবং ছায়ার দৈর্ঘ্য হয় BD
∴DC=30 মিটার ।
ত্রিভূজ ABC থেকে ∠ACB এর পরিপ্রেক্ষিতে পাই
\(\tan45°=\cfrac{AB}{BC}\)
বা, \(1= \cfrac{AB}{BC}\)
বা,\(BC=AB---(i)\)
ত্রিভূজ ABD থেকে ∠ADB এর পরিপ্রেক্ষিতে পাই
\(\tan60°=\cfrac{AB}{BD}\)
বা, \(√3=\cfrac{AB}{BD}\)
বা,\(BD=\cfrac{AB}{√3}---(ii)\)
আবার, \(BC-BD=CD=30\)
বা, \(AB-\cfrac{AB}{√3}=30\)
বা, \(AB(1-\cfrac{1}{\sqrt3})=30\)
বা, \(AB\times \cfrac{\sqrt3-1}{\sqrt3}=30\)
বা, \(AB=30\times \cfrac{\sqrt3}{\sqrt3-1}\)
\(=30\times \cfrac{\sqrt3(\sqrt3+1)}{(\sqrt3-1)(\sqrt3+1)}\)
\(=30\times \cfrac{(3+\sqrt3)}{3-1}\)
\(=15(3+\sqrt3)\)
\(=15\sqrt3(\sqrt3+1)\)
\(\therefore\) স্তম্ভটির উচ্চতা \(=15\sqrt3(\sqrt3+1)\) মিটার
