প্রমাণ করো অর্ধবৃত্তস্থ কোণ এক সমকোণ।
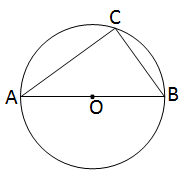
প্রদত্তঃ O কেন্দ্রীয় বৃত্তের \(\angle\)ACB যে-কোনো একটি অর্ধবৃত্তস্থ কোণ ।
প্রমান করতে হবে যেঃ \(\angle\)ACB=1 সমকোণ
প্রমানঃ O কেন্দ্রীয় বৃত্তের \(\overset{ \huge\frown}{APB}\) বৃত্তচাপের দ্বারা গঠিত সম্মুখ কেন্দ্রস্থ কোণটি \(\angle\)AOB এবং \(\angle\)ACB ওই \(\overset{ \huge\frown}{APB}\) বৃত্তচাপের দ্বারা গঠিত সম্মুখ বৃত্তস্থ কোণ ।
\(\therefore \angle\)AOB=2\(\angle\)ACB -------(i)
যেহেতু, AB একটি সরলরেখাংশ, সুতরাং \(\angle\)AOB একটি সরলকোণ ।
\(\therefore \angle\)AOB=2 সমকোণ
সুতরাং, 2\(\angle\)ACB=2 সমকোণ [(i) থেকে পেলাম]
\(\therefore \angle\)ACB=1 সমকোণ [প্রমাণিত]