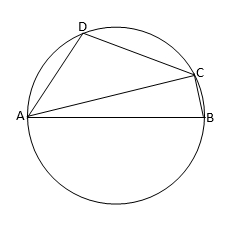
O কেন্দ্রীয় বৃত্তের AB ব্যাস। ABCD বৃত্তস্থ চতুৰ্ভুজ। \(\angle ADC\)=120° হলে, \(\angle BAC\) এর মান (a) \(50^\circ\) (b) \(60^\circ\) (c) \(30^\circ\) (d) \(40^\circ\)
Answer: C
\(\because\) ABCD একটি বৃত্তস্থ চতুর্ভূজ ।
সুতরাং, \(\angle\)ADC+\(\angle\)ABC=180\(^o\)
বা, 120\(^o\) +\(\angle\)ABC=180\(^o\)
বা, \(\angle\)ABC=180\(^o\)-120\(^o\)=60\(^o\)
আবার \(\angle\)ACB = অর্ধবৃত্তস্থ কোণ = 90\(^o\)
\(\therefore \angle\)BAC=180\(^o\)-[\(\angle\)ACB+\(\angle\)ABC]
=180\(^o\)-[90^\(o\)+60\(^o\)]
=180\(^o\)-150\(^o\)
=30\(^o\)
\(\because\) ABCD একটি বৃত্তস্থ চতুর্ভূজ ।
সুতরাং, \(\angle\)ADC+\(\angle\)ABC=180\(^o\)
বা, 120\(^o\) +\(\angle\)ABC=180\(^o\)
বা, \(\angle\)ABC=180\(^o\)-120\(^o\)=60\(^o\)
আবার \(\angle\)ACB = অর্ধবৃত্তস্থ কোণ = 90\(^o\)
\(\therefore \angle\)BAC=180\(^o\)-[\(\angle\)ACB+\(\angle\)ABC]
=180\(^o\)-[90^\(o\)+60\(^o\)]
=180\(^o\)-150\(^o\)
=30\(^o\)