একটি বৃত্তের দুটি জ্যা-এর দৈর্ঘ্যের অনুপাত 4:3। যদি জ্যা দুটির কেন্দ্র থেকে দূরত্ব যথাক্রমে 9 সেমি এবং 12 সেমি হয়, তবে কেন্দ্রের নিকটতম জ্যাটির দৈর্ঘ্য কত হবে?
Loading content...
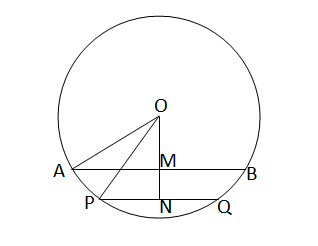
ধরি, O কেন্দ্রীয় বৃত্তটির দুটি জ্যা AB এবং PQ -এর দৈর্ঘ্যের অনুপাত AB:PQ=4:3। এবং জ্যা দুটির কেন্দ্র থেকে দূরত্ব OM=9 সেমি এবং ON=12 সেমি । ধরি, AB\(=4x\) সেমি এবং PQ\(=3x\) সেমি ।
\(\therefore \triangle\)OPN এর
OP\(^2\)=ON\(^2\)+PN\(^2\)
বা, OP\(^2\)=\(12^2\)+\((\cfrac{3x}{2})^2\)
বা, OP\(^2\)=\(144+\cfrac{9x^2}{4}-----(i)\)
এবং \(\triangle\)OAM এর OA\(^2\)=OM\(^2\)+AM\(^2\)
বা, OA\(^2\)=\(9^2\)+\((\cfrac{\cancel42x}{\cancel2})^2\)
বা, OA\(^2\)=\(81+4x^2-----(ii)\)
যেহেতু OA এবং OP উভয়েই বৃত্তের ব্যাসার্ধ সুতরাং \((i)\) এবং \((ii)\) নং সমীকরন থেকে পাই,
\(81+4x^2=144+\cfrac{9x^2}{4}\)
বা, \(4x^2-\cfrac{9x^2}{4}=144-81\)
বা, \(\cfrac{16x^2-9x^2}{4}=63\)
বা, \(7x^2=63\times 4\)
বা, \(x^2=\cfrac{\cancel{63}9\times 4}{\cancel7}\)
বা, \(x=\sqrt{36}=6\)
\(\therefore\) কেন্দ্রের নিকটতম জ্যাটির দৈর্ঘ্য \(=4\times 6\) সেমি \(=24\) সেমি ।
