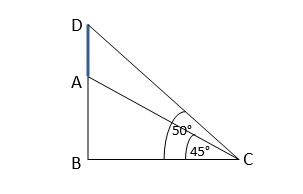
---

ধরি, AB একটি তিনতলা বাড়ির ছাদ A বিন্দুতে AD=3.6 মিটার দৈর্ঘ্যের একটি পতাকা দণ্ড আছে । রাস্তার কোনো একস্থান C বিন্দু থেকে দেখলে পতাকা দণ্ডটির চুড়া D ও পাদদেশ A বিন্দুর উন্নতি কোণ যথাক্রমে \(\angle\)BCD=50° ও \(\angle\)BCA=45°

সমকোণী ত্রিভূজ \(\triangle\)ABC থেকে পাই,
\(\cfrac{AB}{BC}=tan 45^o=1\)
বা, \(AB=BC\)-------(i)

আবার, সমকোণী ত্রিভূজ \(\triangle\)BDC থেকে পাই,
\(\cfrac{BD}{BC}=tan 50^o=1.2\)
বা, \(BD=1.2BC\)-------(ii)

আবার যেহেতু \(BD-AB=AD\)
বা, \(1.2BC-BC=3.6\) [(i) এবং (ii) নং সমীকরন থেকে]
বা, \(0.2BC=3.6\)
বা, \(BC=\cfrac{3.6}{0.2}=\cfrac{36}{2}=18\)

(i) নং সমীকরনে BC এর মান বসিয়ে পাই AB=BC=18 মিটার

\(\therefore\) বাড়িটির উচ্চতা 18 মিটার ।