O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে বৃত্তে দুটি স্পর্শক টানি যারা বৃত্তকে যথাক্রমে B ও C বিন্দুতে স্পর্শ করে। প্রমাণ করি যে, AO, BC-এর লম্বসমদ্বিখণ্ডক।
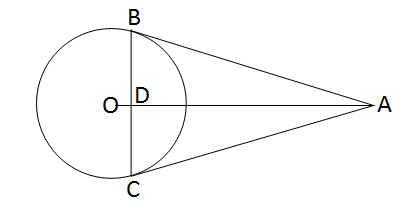
প্রদত্ত : O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু A থেকে বৃত্তে দুটি স্পর্শক টানা হয়েছে যারা বৃত্তকে যথাক্রমে B ও C বিন্দুতে স্পর্শ করেছে । A, O যুক্ত করা হল । AO, BC কে D বিন্দুতে ছেদ করেছে ।
প্রমান করতে হবে যে : AO, BC এর লম্বসমদ্বিখন্ডক ।
প্রমান : O কেন্দ্রীয় বৃত্তের AB ও AC স্পর্শক ।
সুতরাং, AB=AC এবং AO, \(\angle\)BAC এর সমদ্বিখন্ডক ।
অর্থাৎ, \(\angle\)BAD=\(\angle\)CAD
\(\triangle\)ABD এবং \(\triangle\)ACD এর মধ্যে
AB=AC
\(\angle\)BAD=\(\angle\)CAD
এবং AD সাধারন বাহু ।
\(\therefore \triangle\)ABD \(\cong\) \(\triangle\)ACD [S-A-S সর্বসমতার শর্তানুযায়ী]
\(\therefore\) BD=CD [অনুরূপ বাহু]
এবং \(\angle\)BDA=\(\angle\)CDA [অনুরূপ কোণ]
আবার, \(\angle\)BDA+\(\angle\)CDA=180°
বা, 2\(\angle\)BDA=180° [\(\because \angle\)BDA=\(\angle\)CDA]
\(\therefore \angle\)BDA=90°
অর্থাৎ, AD\(\bot\) BC
\(\therefore \) AD, BC এর লম্বসমদ্বিখন্ডক । (প্রমাণিত)