দুটি এককেন্দ্রীয় বৃত্তের বৃহত্তরটির AB ও AC জ্যা দুটি অপর বৃত্তকে যথাক্রমে P ও Q বিন্দুতে স্পর্শ করলে, প্রমাণ করি যে, PQ= \(\frac{1}{2}\)BC.
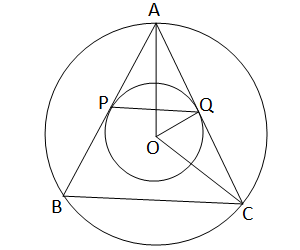
দুটি এককেন্দ্রীয় বৃত্তের বৃহত্তরটির AB এবং AC জ্যা অপর বৃত্তকে P ও Q বিন্দুতে স্পর্শ করেছে।
প্রমান করতে হবে যে,PQ=\(\cfrac{1}{2}\) BC
অঙ্কনঃ ধরি বৃত্তের কেন্দ্র O; O,A;O,C এবং O,Q যুক্ত করা হল।
প্রমানঃ ∆AOQ এবং ∆COQ এর মধ্যে
AO=OC [একই বৃত্তের ব্যাসার্ধ]
\(\angle\)OAQ=\(\angle\)OCQ [∵∆AOC এর AO=OC]
এবং OQ সাধারন বাহু।
∴AQ=QC [অনুরূপ বাহু]
∴∆AOQ ≅ ∆COQ
অর্থাৎ,Q,AC এর মধ্যবিন্দু।
অনুরূপভাবে,OP এবং OB যুক্ত করে প্রমান করা যায় যে,P,AB এর মধ্যবিন্দু।
∴∆ABC এর AB এবং AC বাহুর মধ্যবিন্দু সংযোজক রেখাংশ PQ
সুতরাং PQ=\(\cfrac{1}{2}\) AB [প্রমানিত]