O কেন্দ্রীয় বৃত্তের AB ব্যাস, বৃত্তের উপরিস্থিত কোনো বিন্দু P থেকে PN, AB এর উপর একটা লম্ব টানা হল। O কেন্দ্রীয় বৃত্তের AB ব্যাস, বৃত্তের উপরিস্থিত কোনো বিন্দু P থেকে PN, AB এর উপর একটা লম্ব টানা হল। জ্যামিতিক যুক্তি দিয়ে প্রমাণ করো যে PB\(^2\)=AB×BN Madhyamik 2025
Loading content...
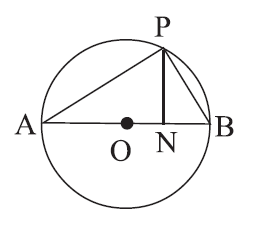
প্রদত্ত : O কেন্দ্রীয় বৃত্তের AB ব্যাস। P বৃত্তের উপরিস্থিত যেকোনো একটি বিন্দু এবং PN\(\bot\)AB
প্রমান করতে হবে : PB\(^2\)=AB.BN
প্রমান : AB বৃত্তের ব্যাস । সুতরাং ∠APB অর্ধবৃত্তস্থ কোণ ।
∴ ∠APB=1 সমকোণ।
সমকোণী ত্রিভূজ APB এর সমকৌণিক বিন্দু P থেকে অতিভূজ AB এর উপর PN লম্ব ।
∴ ∆ABP ও ∆PBN পরস্পর সদৃশ ।
সুতরাং, \(\frac{PB}{BN}=\frac{AB}{PB}\)
∴ PB\(^2\)=AB.BN (প্রমাণিত)