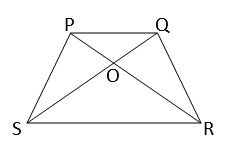
---

\(PQRS\) একটি সামান্তরিক যার, \(PQ∥SR; PR \) ও \(QS\) কর্ণ দুটি \(O\) বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে, \(OP:OR=OQ:OS\) এবং যদি \(SR=2PQ \) হয়,তবে \(O\) কর্ণ দুটির সমত্রিখন্ডক বিন্দুর একটি বিন্দু

প্রমানঃ \(∆POQ\) এবং \(∆OSR\) এর মধ্যে
\(∠OPQ=∠ORS\) [ \(∵PQ∥SR\) এবং \(PR\) ছেদক]
\(∠OQP=∠OSR\) [ \(∵PQ∥SR \) এবং \(QS\) ছেদক]
এবং \(∠POQ=\) বিপ্রতীপ \(∠SOR\)
\(∴∆POQ \) এবং \(∆OSR\) সদৃশকোণী

\(∴ \cfrac{OP}{OR}= \cfrac{OQ}{OS}= \cfrac{PQ}{SR}\)
অর্থাৎ, \( \cfrac{OP}{OR}= \cfrac{OQ}{OS} \)
বা, \(OP:OR=OQ:OS\) (প্রমানিত)

এখন, \(SR=2PQ\) হলে,
\( \cfrac{OP}{OR}= \cfrac{PQ}{SR}= \cfrac{PQ}{2PQ}= \cfrac{1}{2} \)
বা, \(OR=2OP \)
বা, \(OR:OP=2:1\)

এবং \( \cfrac{OQ}{OS}= \cfrac{PQ}{SR}= \cfrac{PQ}{2PQ}= \cfrac{1}{2}\)
বা, \(OS=2OQ \)
বা, \(OS:OQ=2:1 \)

\(∴O\) বিন্দুটি \(PR \) এবং \(QS \) কর্ণদুটির প্রত্যেকটির সমত্রিখন্ডক বিন্দুর একটি বিন্দু হবে। (প্রমানিত)