সমকোণী ত্রিভুজ ABC-এর \(\angle\)A সমকোণ। অতিভুজ BC-এর উপর লম্ব AD হলে, প্রমাণ করি যে, \(\frac{∆ABC}{∆ACD}=\frac{BC^2}{AC^2} \)
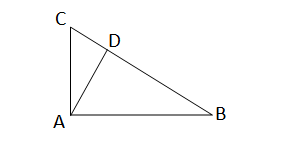
সমকোণী ত্রিভূজ ABC এর \(\angle\)A সমকোণ। অতিভূজ BC এর উপর AD লম্ব হলে প্রমান করতে হবে যে, \(\frac{∆ABC}{∆ACD}=\frac{BC^2}{AC^2}\)
প্রমানঃ যেহেতু CAB সমকোণী ত্রিভূজের সমকৌণিক বিন্দু A থেকে অতিভূজ BC এর উপর AD লম্ব,তাই ∆ACD এবং ∆ABC সদৃশকোণী
∴ \(\frac{AC}{BC}=\frac{CD}{AC}\)
বা, AC\(^2\)=BC.CD
বা, CD\(=\frac{AC^2}{BC}\)---(i)
এখন, \(\frac{∆ABC}{∆ACD}=\frac{\frac{1}{2}.BC.AD}{\frac{1}{2}.CD.AD}=\frac{BC}{CD}\)
\(=\frac{BC}{\frac{AC^2}{BC}}=\frac{BC^2}{AC^2}\)
∴\( \frac {\triangle ABC }{\triangle ACD}=\frac {BC^2}{AC^2} \) (প্রমানিত)