দুটি বৃত্তের একটি অপরটির কেন্দ্র O বিন্দুগামী এবং বৃত্ত দুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা O বিন্দুগামী বৃত্তকে P বিন্দুতে এবং O কেন্দ্রীয় বৃত্তকে R বিন্দুতে ছেদ করেছে। P, B ও R, B যুক্ত করে, প্রমাণ করি যে PR = PB
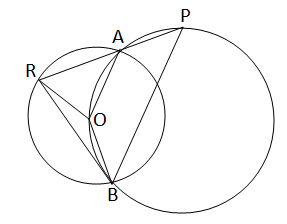
দুটি বৃত্তের একটি অপরটির কেন্দ্র O বিন্দুগামী এবং বৃত্ত দুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা O বিন্দুগামী বৃত্তকে P বিন্দুতে এবং O কেন্দ্রীয় বৃত্তকে R বিন্দুতে ছেদ করেছে। P,Bও R,B যুক্ত করা হল।
প্রমান করতে হবে যে,PR=PB
অঙ্কনঃ O,A;O,R এবং O,B যুক্ত করা হল।
প্রমানঃ ∆ROB এর RO=OB [বৃত্তের ব্যাসার্ধ]
∴\(\angle\)ORB=\(\angle\)OBR---(i)
∆AOR এর OA=OR [ বৃত্তের ব্যাসার্ধ]
∴\(\angle\)ARO=\(\angle\)OAR
আবার চতুর্ভূজ AOBP সমবৃত্তস্থ ।
∴\(\angle\)OBP+\(\angle\)OAP=2 সমকোণ
আবার,PR বাহুর ওপর A বিন্দুতে AO দন্ডায়মান।
∴\(\angle\)OAP+\(\angle\)OAR=2 সমকোণ
∴\(\angle\)OBP=\(\angle\)OAR
∴\(\angle\)ARO=\(\angle\)OBP---(ii)
এখন \(\angle\)PRB=\(\angle\)ARO+\(\angle\)ORB =\(\angle\)OBP+\(\angle\)OBR=\(\angle\)PBR
∴∆PRB এর \(\angle\)PRB=\(\angle\)PBR
∴PR=PB[প্রমানিত]