রুমেলা O কেন্দ্রীয় একটি বৃত্ত অঙ্কন করেছে যার QR একটি জ্যা। Q ও R বিন্দুতে দুটি স্পর্শক অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে। QM বৃত্তের একটি ব্যাস হলে, প্রমাণ করি যে, ∠QPR = 2∠RQM.
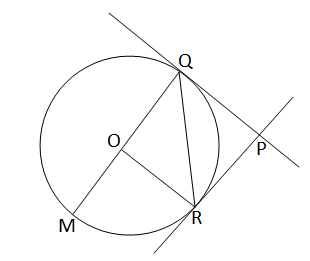
O কেন্দ্রীয় বৃত্তের QR জ্যা। Q ও R বিন্দুতে স্পর্শক দুটি P বিন্দুতে ছেদ করেছে। QM বৃত্তের ব্যাস হলে প্রমান করতে হবে যে,\(\angle\)QPR=2\(\angle\)RQM
অঙ্কনঃ O,R যুক্ত করা হল।
প্রমানঃ যেহেতু RP,R বিন্দুতে এবং QP,Q বিন্দুতে স্পর্শক,
সুতরাং \(\angle\)OQP=\(\angle\)ORP=90°
এখন ∆OQR এর OQ=OR
∴\(\angle\)OQR=\(\angle\)ORQ
আবার ∆PQR থেকে পাই
\(\angle\)QPR+\(\angle\)PQR+\(\angle\)QRP=180°
বা,\(\angle\)QPR+(90°-\(\angle\)OQR)+(90°-\(\angle\)ORQ)=180°
বা,\(\angle\)QPR=\(\angle\)OQR+\(\angle\)ORQ
অর্থাৎ,\(\angle\)QPR=2\(\angle\)OQR [∵\(\angle\)OQR=\(\angle\)ORQ]
∴ \(\angle\)QPR=2\(\angle\)RQM (প্রমানিত)