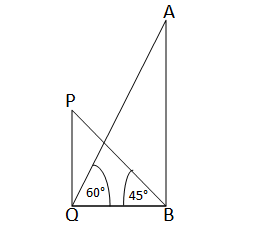
---

দুটি স্তম্ভের উচ্চতা যথাক্রমে AB=\(h_1\) মিটার ও PQ=\(h_2\) মিটার। দ্বিতীয় স্তম্ভের গােড়া Q থেকে প্রথমটির চূড়া Aএর উন্নতি কোণ \(\angle\)AQB=60° এবং প্রথমটির গােড়া B থেকে দ্বিতীয়টির চুড়া P এর উন্নতি কোণ \(\angle\)PBQ=45°

\(\triangle\)ABQ থেকে পাই,
\(\tan 60^o=\cfrac{AB}{BQ}\)
বা, \(\sqrt3=\cfrac{h_1}{BQ}\)
বা, \(BQ=\cfrac{h_1}{\sqrt3}-----(i)\)

আবার, \(\triangle\)PQB থেকে পাই,
\(\tan 45^o=\cfrac{PQ}{BQ}\)
বা, \(1=\cfrac{h_2}{BQ}\)
বা, \(BQ=h_2-----(ii)\)

\((i)\) ও \((ii)\) নং সমীকরন থেকে পাই,
\(\cfrac{h_1}{\sqrt3}=h_2\)
বা, \(h_1=\sqrt3h_2\)
বা, \(h_1^2=3h_2^2\)(প্রমাণিত)