প্রমাণ করি যে, বৃত্তের পরিলিখিত সামান্তরিক মাত্রই রম্বস।
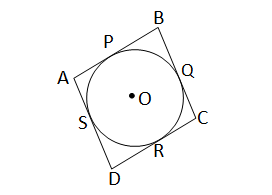
ধরি,O কেন্দ্রীয় বৃত্তের পরিলিখিত একটি সামন্তরিক ABCD; যার বাহুচারটি যথাক্রমে P,Q,R,S বিন্দুতে স্পর্শ করেছে। প্রমান করতে হবে যে ABCD একটি রম্বস,অর্থাৎ AB=AD
প্রমানঃ যেহেতু বহিঃস্থ A বিন্দু থেকে AP এবং AS দুটি স্পর্শক,তাই AP=AS;
অনুরূপভাবে,BP=BQ, CQ=CR,DR=DS
সুতরাং AB+CD = AP + BP + CR + DR = AS + BQ + CQ + DS = AS + DS + BQ + CQ = AD + BC
[∵ABCD একটি সামন্তরিক, সুতরাং AB=CD এবং AD=BC]
∴AB+AB=AD+AD
অথবা,2AB=2AD
∴AB=AD (প্রমানিত)