একটি বৃত্তে ABC ত্রিভুজটি অন্তর্লিখিত। AX, BY এবং CZ যথাক্রমে \(\angle\)BAC, \(\angle\)ABCও\(\angle\)ACB -এর সমদ্বিখণ্ডক এবং বৃত্তে যথাক্রমে X, Yও Z বিন্দুতে মিলিত হয়। প্রমাণ করি যে, AX,YZ-এর উপর লম্ব।
Loading content...
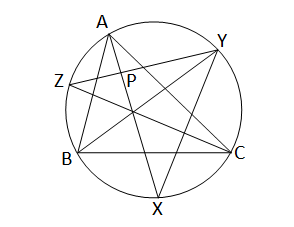
∆ABC বৃত্তের আন্তর্লিখিত। AX,BY এবং CZ যথাক্রমে \(\angle\)BAC,\(\angle\)ABC ও \(\angle\)ACB এর সমদ্বিখন্ডক ত্রয় যথাক্রমে X,Y,Z বিন্দুতে মিলিত হয়।
প্রমান করতে হবে যে,AX,YZ এর ওপর লম্ব।
অঙ্কনঃ X,Y যুক্ত করা হল।
প্রমানঃ AY চাপের ওপর অবস্থিত দুটি বৃত্তস্থ কোণ
\(\angle\)AXY এবং \(\angle\)ABY
∴\(\angle\)AXY=\(\angle\)ABY---(i)
আবার,BZ চাপের ওপর অবস্থিত দুটি বৃত্তস্থ কোণ
\(\angle\)BYZ এবং \(\angle\)BCZ
∴\(\angle\)BYZ=\(\angle\)BCZ---(ii)
আবার,BX চাপের ওপর অবস্থিত দুটি বৃত্তস্থ কোণ
\(\angle\)BYX এবং \(\angle\)BAX
∴\(\angle\)BYX=\(\angle\)BAX---(iii)
এখন ∆PXY এর,
\(\angle\)PYX+\(\angle\)PXY=\(\angle\)BYZ+\(\angle\)BYX+\(\angle\)AXY =\(\angle\)BCZ+\(\angle\)BAX+\(\angle\)ABY [(ii),(iii) (i)নং সমীকরনের মান বসিয়ে]
=\(\frac{1}{2}\)\(\angle\)BCA+\(\frac{1}{2}\)\(\angle\)BAC+\(\frac{1}{2}\)\(\angle\)ABC
=\(\frac{1}{2}\) ( \(\angle\)BCA+\(\angle\)BAC+\(\angle\)ABC)=\(\frac{180°}{2}\)=90°
∴\(\angle\)XPY=180°-(\(\angle\)PYX+\(\angle\)PXY)=180°-90°=90°
অর্থাৎ,AX,YZ এর ওপর লম্ব । (প্রমানিত)
