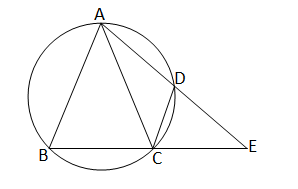
---

ধরি,∆ABC এর AB=AC এবং বর্ধিত BC এর ওপর E একটি বিন্দু। ∆ABC এর পরিবৃত্ত AE কে D বিন্দুতে ছেদ করেছে।

প্রমান করতে হবে যে,\(\angle\)ACD=\(\angle\)AEC

অঙ্কনঃ C,D যুক্ত করা হল।

প্রমানঃ বৃত্তস্থ চতুর্ভূজ ABCD এর
\(\angle\)ABC+\(\angle\)ADC=2 সমকোণ (বিপরীত কোণ)
আবার AE সরলরেখার ওপর D বিন্দুতে CD দন্ডায়মান।
∴\(\angle\)CDE+\(\angle\)ADC=2 সমকোণ
অর্থাৎ,\(\angle\)ABC+\(\angle\)ADC= \(\angle\)CDE+\(\angle\)ADC
বা, \(\angle\)ABC=\(\angle\)CDE---(i)

আবার ∆ABC এর AB=AC,
অর্থাৎ \(\angle\)ABC=\(\angle\)ACB---(ii)

∆CDE এর EC বাহু B পর্যন্ত বর্ধিত
∴\(\angle\)DCB=\(\angle\)CDE+\(\angle\)DEC
বা, \(\angle\)ACD+\(\angle\)ACB= \(\angle\)CDE+\(\angle\)DEC
বা,\(\angle\)ACD+\(\angle\)ACB= \(\angle\)ABC+\(\angle\)DEC [(i)নং সমীকরনের মান বসিয়ে ]
বা, \(\angle\)ACD+\(\angle\)ACB= \(\angle\)ACB+\(\angle\)DEC [(ii)নং সমীকরনের মান বসিয়ে ]
বা, \(\angle\)ACD=\(\angle\)DEC

∴∠ACD=∠AEC (প্রমানিত)