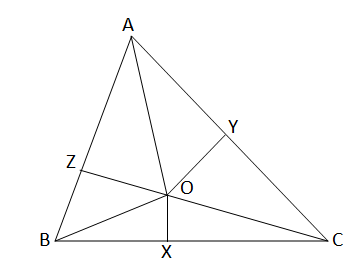
---

ABC ত্রিভূজের অভ্যন্তরস্থ বিন্দু O থেকে BC,CA ও AB এর উপর OX,OY ও OZ লম্ব। প্রমান করতে হবে যে,AZ\(^2\)+BX\(^2\)+CY\(^2\)=AY\(^2\)+CX\(^2\)+BZ\(^2\)

অঙ্কনঃ O,A; O,B এবং O,C যুক্ত করা হল।

প্রমানঃ পিথাগোরাসের সূত্র থেকে
সমকোণী ∆AOZ থেকে পাই,AZ\(^2\)+OZ\(^2\)=OA\(^2\)
বা,AZ\(^2\)=OA\(^2\)-OZ\(^2\)---(i)

সমকোণী ∆BOX থেকে পাই,BX\(^2\)+OX\(^2\)=OB\(^2\)
বা,BX\(^2\)=OB\(^2\)-OX\(^2\)---(ii)

সমকোণী ∆COY থেকে পাই,CY\(^2\)+OY\(^2\)=OC\(^2\)
বা,CY\(^2\)=OC\(^2\)-OY\(^2\)---(iii)

(i),(ii)ও (iii)নং সমীকরন থেকে পাই
AZ\(^2\)+BX\(^2\)+CY\(^2\)
=OA\(^2\)-OZ\(^2\)+OB\(^2\)-OX\(^2\)+OC\(^2\)-OY\(^2\)
=OA\(^2\)-OY\(^2\)+OC\(^2\)-OX\(^2\)+OB\(^2\)-OZ\(^2\)
=AY\(^2\)+CX\(^2\)+BZ\(^2\) [∵∆AOY,∆COX,∆BOZ সমকোণী ত্রিভূজ]

∴AZ\(^2\)+BX\(^2\)+CY\(^2\)=AY\(^2\)+CX\(^2\)+BZ\(^2\) (প্রমানিত)