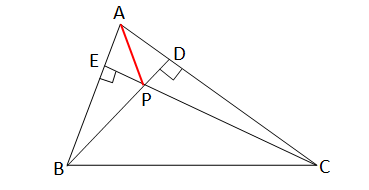
---

ধরি,ABC ত্রিভূজের AC>AB এবং শীর্ষবিন্দু B ও C থেকে AC এবং AB এর ওপর লম্ব যথাক্রমে BD ও CE পরস্পরকে P বিন্দুতে ছেদ করেছে।

প্রমান করতে হবে যে AC\(^2\)+BP\(^2\)=AB\(^2\)+CP\(^2\)

অঙ্কনঃ A,P যুক্ত করা হল ।

প্রমানঃ সমকোণী ∆BEC থেকে পিথাগোরাসের সূত্র থেকে পাই BC\(^2\)=BE\(^2\)+EC\(^2\)---(i)

সমকোণী ∆BDC থেকে পিথাগোরাসের সূত্র থেকে পাই,BC\(^2\)=BD\(^2\)+DC\(^2\)---(ii)

(i)এবং (ii)নং সমীকরন থেকে BC\(^2\) এর মান তুলনা করে পাই,BE\(^2\)+EC\(^2\)=BD\(^2\)+DC\(^2\)---(iii)

সমকোণী ত্রিভূজ ∆AEP থেকে পিথাগোরাসের সূত্র থেকে পাই,AP\(^2\)=AE\(^2\)+EP\(^2\)---(iv)

সমকোণী ত্রিভূজ ∆ADP থেকে পিথাগোরাসের সূত্র থেকে পাই,AP\(^2\)=AD\(^2\)+DP\(^2\)---(v)

(iv)এবং (v)নং সমীকরন থেকে AP\(^2\) এর মান তুলনা করে পাই,AE\(^2\)+EP\(^2\)=AD\(^2\)+DP\(^2\)---(vi)

(iii)এবং (iv)নং সমীকরনের উভয়পক্ষ যোগ করে পাই,
BE\(^2\)+EC\(^2\)+AE\(^2\)+EP\(^2\)=BD\(^2\)+DC\(^2\)+AD\(^2\)+DP\(^2\)
বা,BE\(^2\)+EP\(^2\)+EC\(^2\)+AE\(^2\)=BD\(^2\)+AD\(^2\)+DC\(^2\)+DP\(^2\)

\([\) পিথাগোরাসের সূত্র থেকে
∆BPE থেকে পাই BE\(^2\)+EP\(^2\)=BP\(^2\)
∆AEC থেকে পাই EC\(^2\)+AE\(^2\)=AC\(^2\)
∆ADB থেকে পাই BD\(^2\)+AD\(^2\)=AB\(^2\)
∆DPC থেকে পাই DC\(^2\)+DP\(^2\)= CP\(^2\)\(]\)

বা,BP\(^2\)+AC\(^2\)=AB\(^2\)+CP\(^2\) (প্রমানিত)