তিমির দুটি বৃত্ত এঁকেছে যারা পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। P বিন্দু দিয়ে দুটি সরলরেখা টানলাম যারা একটি বৃত্তকে A, B বিন্দুতে এবং অপর বৃত্তকে যথাক্রমে C, D বিন্দুতে ছেদ করল। প্রমাণ করি যে \(\angle\)AQC = \(\angle\)BQD
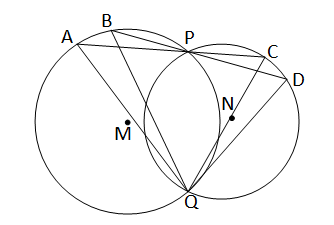
ধরি,M এবং N কেন্দ্রীয় দুটি বৃত্ত পরস্পরকে P এবং Q বিন্দুতে ছেদ করেছে। P বিন্দুতে দুটি সরলরেখা M কেন্দ্রীয় বৃত্তকে যথাক্রমে A,B এবং N কেন্দ্রীয় বৃত্তকে C,D বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে, \(\angle\)AQC=\(\angle\)BQD
প্রমানঃ∵Mকেন্দ্রীয় বৃত্তের ক্ষেত্রে,
\(\angle\)PAQ=\(\angle\)PBQ [∵একই বৃত্তাংশের ওপর অবস্থিত]
আবার N কেন্দ্রীয় বৃত্তের ক্ষেত্রে,\(\angle\)PCQ=\(\angle\)PDQ [∵একই বৃত্তাংশের ওপর অবস্থিত]
∴\(\angle\)PAQ+\(\angle\)PCQ=\(\angle\)PBQ+\(\angle\)PDQ--(i)
∆ACQ এর ক্ষেত্রে,
\(\angle\)AQC=180°-(\(\angle\)PAQ+\(\angle\)PCQ) =180°-(\(\angle\)PBQ+\(\angle\)PDQ) [(i)নং সমীকরনের মান বসিয়ে]
=\(\angle\)BQD (প্রমানিত)