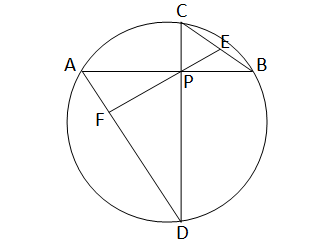
---

AB এবং CD জ্যা দুটি পরস্পরকে P বিন্দুতে ছেদ করেছে। P বিন্দু দিয়ে AD এর ওপর লম্ব PF;FP কে বর্ধিত করলে তা BC কে E বিন্দুতে ছেদ করে।
প্রমান করতে হবে যে,E,BC এর মধ্যবিন্দু।

প্রমানঃ ∆FPD এর PF⊥FD
সুতরাং,\(\angle\)FPD=90°-\(\angle\)FDP
আবার,∆APD এর AP⊥PD
সুতরাং,\(\angle\)PAD=90°-\(\angle\)ADP
∴\(\angle\)FPD=\(\angle\)PAD---(i)

অনুরূপভাবে,\(\angle\)APF=\(\angle\)FDP---(ii)

AC বৃত্তাংশের ওপর অবস্থিত দুটি কোণ
\(\angle\)ADC=\(\angle\)ABC
এবং DB বৃত্তাংশের ওপর অবস্থিত দুটি কোণ
\(\angle\)DAB=\(\angle\)BCD

∆CPE এর
\(\angle\)PCE=\(\angle\)PAD [একই বৃত্তাংশের কোণ]
\(\angle\)CPE=বিপ্রতীপ \(\angle\)FPD=\(\angle\)PAD [(i)নং সমীকরন থেকে]
∴\(\angle\)PCE=\(\angle\)CPE
সুতরাং,CE=PE---(iii)

∆PEB এর
\(\angle\)EBP=\(\angle\)ADC [একই বৃত্তাংশের কোণ]
\(\angle\)BPE=বিপ্রতীপ \(\angle\)APF=\(\angle\)FDP [(ii)নং সমীকরন থেকে]
∴ \(\angle\)EBP=\(\angle\)BPE
সুতরাং,BE=PE---(iv)

(iii)এবং (iv)নং সমীকরন থেকে পাই,
CE=BE

∴E,BC এর মধ্যবিন্দু (প্রমানিত)।