∆ABC-এর BC বাহুর সমান্তরাল সরলরেখা AB ও AC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে। PB-এর দৈর্ঘ্য AP-এর দৈর্ঘ্যের দ্বিগুণ এবং QC-এর দৈর্ঘ্য AQ-এর দৈর্ঘ্যের চেয়ে 3 একক বেশি হলে, AC-এর দৈর্ঘ্য কত হবে, হিসাব করে লিখি।
Loading content...
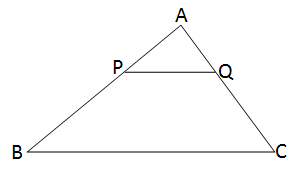
\(\triangle ABC\) এর \(PQ\parallel BC\) এবং \(PB=2AP\) ও \(QC=AQ+3\)
\(\because \triangle ABC\) এর \(PQ \parallel BC\)
\(\therefore \cfrac{AP}{PB}=\cfrac{AQ}{QC}\)
\(\therefore \cfrac{AP}{2AP}=\cfrac{AQ}{AQ+3}\)
বা, \(\therefore \cfrac{AQ}{AQ+3}=\cfrac{1}{2}\)
বা, \(\therefore 2AQ=AQ+3\)
বা,\(AQ=3\)
\(\therefore QC=AQ+3=3+3=6\)
\(\therefore AC=AQ+QC=3+6=9\) একক