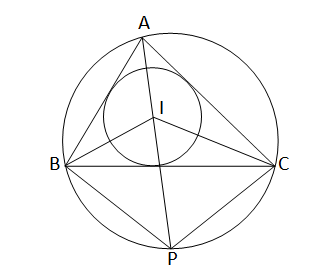
---

∆ABC এর অন্তঃকেন্দ্র I এবং বর্ধিত AI,∆ABC এর পরিবৃত্তকে P বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,PB=PC=PI

অঙ্কনঃ P,B;P,C;B,I এবং C,I যুক্ত করা হল।

প্রমানঃ∵I,∆ABC এর অন্তঃকেন্দ্র সুতরাং,AI,BI ও CI ত্রিভূজের তিনটি কোণের সমদ্বিখন্ডক ।

∆ABC এর পরিবৃত্তের PC বৃত্তাংশে অবস্থিত দুটি বৃত্তস্থ কোণ \(\angle\)PBC এবং \(\angle\)PAC
∴\(\angle\)PBC=\(\angle\)PAC

আবার \(\angle\)PAC=\(\frac{1}{2}\)\(\angle\)BAC [∵AP,\(\angle\)BAC এর সমদ্বিখন্ডক]
∴\(\angle\)PBC=\(\frac{1}{2}\)\(\angle\)BAC
এখন \(\angle\)IBP=\(\angle\)IBC+\(\angle\)PBC =\(\frac{1}{2}\)\(\angle\)ABC+\(\frac{1}{2}\)\(\angle\)BAC---(i)

আবার,∆ABI এর
বহিঃস্থ \(\angle\)BIP=\(\angle\)IBA+\(\angle\)IAB =\(\frac{1}{2}\)\(\angle\)ABC+\(\frac{1}{2}\)\(\angle\)BAC---(ii)

∴(i)এবং (ii)নং সমীকরন থেকে পাই,
\(\angle\)IBP=\(\angle\)BIP

∴∆IBP এর \(\angle\)IBP=\(\angle\)BIP
∴PB=PI
অনুরূপভাবে ∆IPC থেকে প্রমান করা যায় যে PC=PI

∴PB=PC=PI (প্রমানিত)