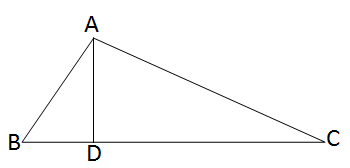
---

\(\triangle\)BDA ও \(\triangle\)ADC এর মধ্যে
\(\angle\)BDA = \(\angle\)ADC = 90° [\(\because\) AD \(\bot\) BC]
এবং \(\frac{BD}{AD}=\frac{AD}{DC}\)
\(\therefore \triangle\)BDA ও \(\triangle\)ADC সদৃশ।
[যেহেতু দুটি ত্রিভুজের একটির একটি কোণ অপরটির একটি কোণের সমান হলে এবং কোণগুলির ধারক বাহুগুলি সমানুপাতী হলে, ত্রিভুজদ্বয় সদৃশ হয়]
সুতরাং, \(\angle\)ABD = \(\angle\)CAD এবং \(\angle\)BAD= \(\angle\)ACD
\(\therefore \angle\)ABD+ \(\angle\)ACD= \(\angle\)CAD+ \(\angle\)BAD
বা, \(\angle\)B + \(\angle\)C = \(\angle\)A
বা, \(\angle\)A + \(\angle\)B+ \(\angle\)C = 2\(\angle\)A
বা, 2\(\angle\)A = 180°
\(\therefore \angle\)A = 90° অর্থাৎ, \(\triangle\)ABC একটি সমকোণী ত্রিভুজ।