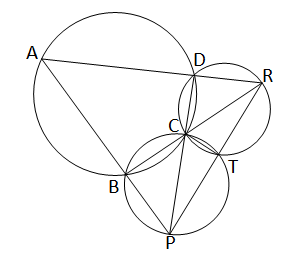
---

ABCD একটি বৃত্তস্থ চতুর্ভূজ,যার বর্ধিত AB এবং DC পরস্পরকে P বিন্দুতে এবং বর্ধিত AD এবং BC পরস্পরকে R বিন্দুতে মিলিত হয়েছে। ∆BPC এবং ∆CDR এর পরিবৃত্তদ্বয় T বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,P,T,R সমরেখ।

অঙ্কনঃ P,T;R,T এবং C,T যুক্ত করা হল।

প্রমানঃ BCTP একটি বৃত্তস্থ চতুর্ভূজ ।
∴\(\angle\)CTP+\(\angle\)CBP=180°
বা,\(\angle\)CTP=180°-\(\angle\)CBP=\(\angle\)ABC [∵AP বাহুর ওপর BC দন্ডায়মান]

আবার,CDRT একটি বৃত্তস্থ চতুর্ভূজ ।
∴\(\angle\)CTR+\(\angle\)CDR=180°
বা,\(\angle\)CTR=180°-\(\angle\)CDR=\(\angle\)CDA [∵AR বাহুর ওপর DC দন্ডায়মান]

এখন,\(\angle\)CTP+\(\angle\)CTR=\(\angle\)ABC+\(\angle\)CDA =2 সমকোণ [∵ABCD বৃত্তস্থ চতুর্ভূজ]

যেহেতু \(\angle\)CTP এবং \(\angle\)CTR এর CT সাধারন বাহু এবং কোণ দুটির সমষ্টি 2 সমকোণ,
∴P,T,R সমরেখ। (প্রমানিত)