X ও Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করেছে । XY-এর মধ্যবিন্দু S-এর সঙ্গে A বিন্দু যুক্ত করলাম এবং A বিন্দু দিয়ে SA-এর উপর লম্ব অঙ্কন করলাম যা বৃত্ত দুটিকে P ও Q বিন্দুতে ছেদ করল । প্রমান করি যে PA=AQ.
Loading content...
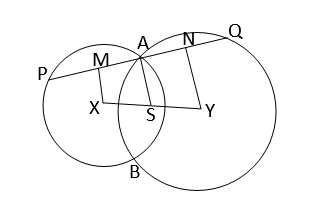
ধরি,X এবং Y কেন্দ্রীয় বৃত্ত পরস্পরকে A এবং B বিন্দুতে ছেদ করেছে। XY এর মধ্যবিন্দু S এবং A যুক্ত করা হল। A বিন্দু দিয়ে SA এর ওপর অঙ্কিত লম্ব বৃত্ত দুটিকে যথাক্রমে P এবং Q বিন্দুতে ছেদ করেছে।
প্রমান করতে হবে যে,PA=AQ
অঙ্কনঃ X এবং Y বিন্দু দিয়ে PQ এর ওপর যথাক্রমে XM এবং YN লম্ব অঙ্কন করা হল।
প্রমানঃ অঙ্কন অনুসারে,XM,SA,YN সরলরেখা তিনটি প্রত্যেকে একই সরলরেখা PQ এর ওপর লম্ব। সুতরাং,XM∥SA∥YN
যেহেতু XM এবং YN রেখাংশ দুটি X এবং Y কেন্দ্রীয় বৃত্তের দুটি জ্যা PA এবং AQ এর উপর লম্ব (অঙ্কনানুসারে),তাই M ও N যথাক্রমে PA এবং AQ এর মধ্যবিন্দু ।
∴MA=\(\cfrac{1}{2}\) PA এবং AN=\(\cfrac{1}{2}\) AQ
আবার যেহেতু S,XY এর মধ্যবিন্দু,সুতরাং XS=SY
অর্থাৎ,XM,SA,YN সমান্তরাল সরলরেখা তিনটি XY থেকে সমান দুটি অংশ ছিন্ন করে।
∴তা অপর সরলরেখা PQ থেকেও সমান দুটি অংশ ছিন্ন করবে।
অর্থাৎ,MA=AN
বা,\(\cfrac{1}{2}\) PA=\(\cfrac{1}{2}\) AQ [∵MA=\(\cfrac{1}{2}\) PA; AN=\(\cfrac{1}{2}\) AQ]
অর্থাৎ,PA=AQ (প্রমানিত)