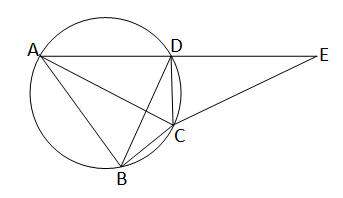
---

ABCD একটি বৃত্তস্থ চতুর্ভূজ এবং AC,\(\angle\)BAD কে সমদ্বিখন্ডিত করেছে। AD কে E পর্যন্ত বাড়ানো হল যাতে,DE=AB হয়।
প্রমান করতে হবে যে, CE=CA

অঙ্কনঃ BD যুক্ত করা হল ।

প্রমানঃ \(\angle\)BAC=\(\angle\)BDC [উভয়েই BC চাপের ওপর অবস্থিত]
এবং \(\angle\)CAD=\(\angle\)DBC [উভয়েই DC চাপের ওপর অবস্থিত]
আবার,\(\angle\)BAC=\(\angle\)CAD [∵AC,\(\angle\)BAD এর সমদ্বিখন্ডক]
∴\(\angle\)BDC=\(\angle\)DBC
∴∆BCD থেকে পাই CD=BC

∵AE সরলরেখার ওপর D বিন্দুতে DE দন্ডায়মান
∴ \(\angle\)EDC+\(\angle\)ADC=2 সমকোণ
আবার,\(\angle\)ADC+\(\angle\)ABC=2 সমকোণ [∵ABCD বৃত্তস্থ চতুর্ভূজ]
∴\(\angle\)EDC+\(\angle\)ADC= \(\angle\)ADC+\(\angle\)ABC
অর্থাৎ,\(\angle\)EDC=\(\angle\)ABC

এখন,∆DCE এবং ∆ABC এর মধ্যে
DE=AB (প্রদত্ত)
\(\angle\)EDC=\(\angle\)ABC (পূর্বে প্রমানিত)
CD=BC (পূর্বে প্রমানিত)
∴∆DCE≅∆ABC [S-A-S অনুসারে]

∴ CE=CA(অনুরূপ বাহু)[প্রমানিত]