একটি চিমনির সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখায় কোনো এক বিন্দু থেকে চিমনির দিকে 50 মিটার এগিয়ে যাওয়ায় তার চূড়ার উন্নতি কোণ 30° থেকে 60° হলো। চিমনির উচ্চতা হিসাব করে লিখি।
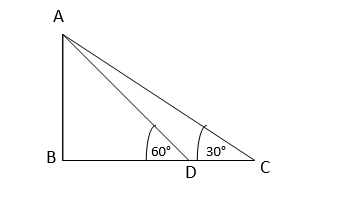
ধরি,AB একটি চিমনি,C বিন্দু থেকে চিমনির চূড়া A বিন্দুর উন্নতি কোণ ∠ACB=30° এবং C বিন্দু থেকে 50 মিটার এগিয়ে D বিন্দু থেকে চিমনির চূড়ার উন্নতি কোণ ∠ADB=60°
সমকোণী ত্রিভূজ ABC থেকে পাই
\(tan30°= \cfrac{AB}{BC}\)
বা, \(\cfrac{1}{√3}=\cfrac{AB}{BC}\)
বা, \(AB=\cfrac{BC}{√3}----(i)\)
সমকোণী ত্রিভূজ ABD থেকে পাই
\(tan60°= \cfrac{AB}{BD}\)
বা, \(√3=\cfrac{AB}{BD}\)
বা, \(AB=BD√3----(ii)\)
\((i)\) এবং \((ii)\) নং সমীকরনে AB এর মানের তুলনা করে পাই
\(\cfrac{BC}{√3}=BD√3\)
বা, \(3BD=BC\)
বা, \(3BD=BD+DC \)
বা, \(3BD-BD=DC \)
বা, \(2BD=50 \)
বা, \(BD=\cfrac{50}{2}=25\)
\((ii)\) নং সমীকরনে BD এর মান বসিয়ে পাই
\(AB=25√3\)
∴চিমনির উচ্চতা \(25√3\) মিটার ।