প্রমাণ করাে, কোনাে বৃত্তের দুটি সমান জ্যা কেন্দ্র থেকে সমদূরবর্তী।
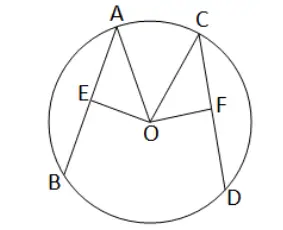
প্রদত্ত : O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা। কেন্দ্র O থেকে AB ও CD এর দূরত্ব যথাক্রমে OE ও OF অর্থাৎ OE ⊥ AB এবং OF ⊥ CD
প্রমান করতে হবে : OE=OF
অঙ্কন : O,A ও O,C যুক্ত করা হল।
প্রমান : OE ⊥ AB এবং OF ⊥ CD (প্রদত্ত)
∴ AE=\(\cfrac{1}{2}\) AB এবং CF=\(\cfrac{1}{2}\)CD
[যেহেতু,বৃত্তের কেন্দ্র থেকে ব্যাস নয় এরূপ কোনো জ্যাএর উপর লম্ব জ্যা টিকে সমদ্বিখন্ডিত করে)]
আবার, AB=CD [প্রদত্ত]
∴ AE=CF----(i)
∴ সমকোণী ∆AEO ও সমকোণী ∆OFC -তে
∠OEA=∠OFC [প্রত্যেকটি সমকোণ]
অতিভূজ OA= অতিভূজ OC [একই বৃত্তের ব্যাসার্ধ]
AE=CF [(i) থেকে পাই]
∆AEO ≅ ∆CFO [R-H-S সর্বসমতার শর্তানুসারে]
∴ OE=OF (প্রমানিত)