10 সেমি. বাহুবিশিষ্ট কোনো রম্বসের একটি কর্ণের দৈর্ঘ্য 12 সেমি. হলে, রম্বসটির অপর কর্ণের দৈর্ঘ্য হিসাব করে লিখি।
Loading content...
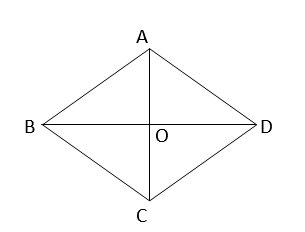
ধরি,ABCD রম্বসের বাহুগুলির দৈর্ঘ্য 10 সেমি,এবং একটি কর্ণ AC=12 সেমি। যেহেতু রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে,
তাই সমকোণী ত্রিভূজ AOD এর
AO\(^2\)+OD\(^2\)=AD\(^2\) [পিথাগোরাসের সূত্র থেকে]
বা,OD\(^2\)=AD\(^2\)-AO\(^2\)=10\(^2\)-6\(^2\)=100-36=64
বা,OD=8
∴BD=2×8 সেমি=16 সেমি।
∴রম্বসের অপর কর্ণটির দৈর্ঘ্য 16 সেমি।