ΔABC-এর A বিন্দু থেকে BC বাহুর উপর অঙ্কিত লম্ব BC বাহুকে D বিন্দুতে এবং B বিন্দু থেকে CA বাহুর উপর অঙ্কিত লম্ব CA বাহুকে E বিন্দুতে ছেদ করে। প্রমাণ করি যে, A, B, D, E বিন্দু চারটি সমবৃত্তস্থ।
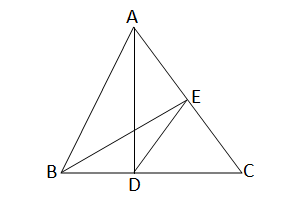
∆ABC এর A বিন্দু থেকে BC বাহুর উপর অঙ্কিত লম্ব BC বাহুকে D বিন্দুতে এবং B বিন্দু থেকে CA বাহুর উপর অঙ্কিত লম্ব CA বাহুকে E বিন্দুতে ছেদ করে।
প্রমান করতে হবে যে,A,B,D,E সমবৃত্তস্থ।
অঙ্কনঃ D,E যুক্ত করা হল।
প্রমানঃ ∆EBC এবং ∆ADC থেকে পাই,
\(\angle\)BEC=\(\angle\)ADC=1 সমকোণ
\(\angle\)ECD সাধারন কোণ
∴অবশিষ্ট \(\angle\)EBC=অবশিষ্ট \(\angle\)DAC
অর্থাৎ,\(\angle\)EBD=\(\angle\)DAE
যেহেতু,DE রেখাংশের একই পার্শ্বে অপর দুই বিন্দু B এবং A তে দুটি সমান কোণ উৎপন্ন করেছে,তাই A,B,D,E সমবৃত্তস্থ (প্রমানিত)